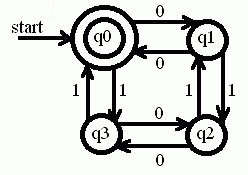
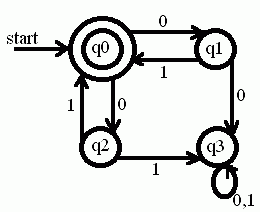
A deterministic finite state automaton (DFA) is a simple language recognition device. It can be seen as a state machine where for each pair of state and input symbol there is one and only one transition to a next state. It will take in a string of input symbols and then for each symbol it will transition to another state according to a transition function. More about DFA can be found here.
Examples from [1]:
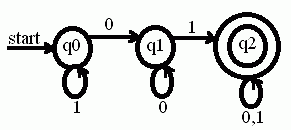
1) Construct a DFA to accept a string containing a zero followed by a one.
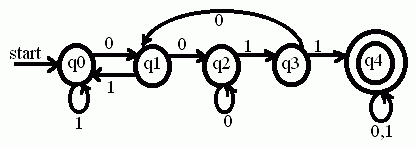
2) Construct a DFA to accept a string containing two consecutive zero’s followed by two consecutive ones.
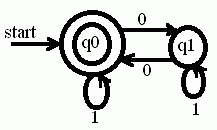
3) Construct a DFA to accept a string containing even number of zeros and any number of ones.
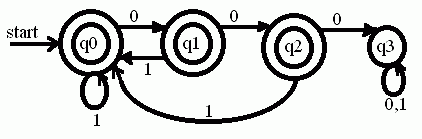
4) Construct a DFA to accept all stings which do not contain three consecutive zeros.
5) Construct a DFA to accept all strings containing even number of zeros and even number of ones.
6) Construct a DFA to accept all strings which satisfy #(x)mod5=2.
7) Construct a DFA to accept all strings (0+1)* with an equal number of zeros and ones such that each prefix has at most one more zero than ones and at most one more one than zeros.
—